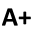8. A local real estate investor in Orlando is considering three alternative investments: a motel, a restaurant, or a theater. Profits from the motel or restaurant will be affected by the availability of gasoline and the number of tourists; profits from the theater will be relatively stable under any conditions. The following payoff table shows the profit or loss that could result from each investment:
|
|
Gasoline Availability |
||
|
Investment |
Shortage |
Stable Supply |
Surplus |
|
Motel |
$-8,000 |
$15,000 |
$20,000 |
|
Restaurant |
2,000 |
8,000 |
6,000 |
|
Theater |
6,000 |
6,000 |
5,000 |
Determine the best investment, using the following decision criteria.
a. Maximax
b. Maximin
c. Minimax regret
d. Hurwicz (α = 0.4)
e. Equal likelihood
16. A concessions manager at the Tech versus A&M football game must decide whether to have the vendors sell sun visors or umbrellas. There is a 30% chance of rain, a 15% chance of overcast skies, and a 55% chance of sunshine, according to the weather forecast in College Junction, where the game is to be held. The manager estimates that the following profits will result from each decision, given each set of weather conditions:
|
|
Weather Conditions |
||
|
Decision |
Rain |
Overcast |
Sunshine |
|
|
.30 |
.15 |
.55 |
|
Sun visors |
$-500 |
$-200 |
$1,500 |
|
Umbrellas |
2,000 |
0 |
-900 |
a. Compute the expected value for each decision and select the best one.
b. Develop the opportunity loss table and compute the expected opportunity loss for each decision.
24. In Problem 13 the Place-Plus real estate development firm has hired an economist to assign a probability to each direction interest rates may take over the next 5 years. The economist has determined that there is a .50 probability that interest rates will decline, a .40 probability that rates will remain stable, and a .10 probability that rates will increase.
a. Using expected value, determine the best project.
b. Determine the expected value of perfect information.
Reference Problem 13: Place-Plus, a real estate development firm, is considering several alternative development projects. These include building and leasing an office park, purchasing a parcel of land and building an office building to rent, buying and leasing a warehouse, building a strip mall, and building and selling condominiums. The financial success of these projects depends on interest rate movement in the next 5 years. The various development projects and their 5-year financial return (in $1,000,000s) given that interest rates will decline, remain stable, or increase, are shown in the following payoff table:
|
|
|
Interest Rate |
|
|
Project |
Decline |
Stable |
Increase |
|
Office park |
$0.5 |
$1.7 |
$4.5 |
|
Office building |
1.5 |
1.9 |
2.5 |
|
Warehouse |
1.7 |
1.4 |
1.0 |
|
Mall |
0.7 |
2.4 |
3.6 |
|
Condominiums |
3.2 |
1.5 |
0.6 |
32. The director of career advising at Orange Community College wants to use decision analysis to provide information to help students decide which 2-year degree program they should pursue. The director has set up the following payoff table for six of the most popular and successful degree programs at OCC that shows the estimated 5-year gross income ($) from each degree for four future economic conditions:
|
|
Economic Conditions |
|||
|
Degree Program |
Recession |
Average |
Good |
Robust |
|
Graphic design |
145,000 |
175,000 |
220,000 |
260,000 |
|
Nursing |
150,000 |
180,000 |
205,000 |
215,000 |
|
Real estate |
115,000 |
165,000 |
220,000 |
320,000 |
|
Medical technology |
130,000 |
180,000 |
210,000 |
280,000 |
|
Culinary technology |
115,000 |
145,000 |
235,000 |
305,000 |
|
Computer information technology |
125,000 |
150,000 |
190,000 |
250,000 |
Determine the best degree program in terms of projected income, using the following decision criteria:
a. Maximax
b. Maximin
c. Equal likelihood
d. Hurwicz (α = 0.50)
36. Construct a decision tree for the decision situation described in Problem 25 and indicate the best decision.
Reference Problem 25: Fenton and Farrah Friendly, husband-and-wife car dealers, are soon going to open a new dealership. They have three offers: from a foreign compact car company, from a U.S. producer of full-sized cars, and from a truck company. The success of each type of dealership will depend on how much gasoline is going to be available during the next few years. The profit from each type of dealership, given the availability of gas, is shown in the following payoff table:
|
|
Gasoline Availability |
|
|
Dealership |
Shortage |
Surplus |
|
|
.6 |
.4 |
|
Compact cars |
$ 300,000 |
$150,000 |
|
Full-sized cars |
-100,000 |
600,000 |
|
Trucks |
120,000 |
170,000 |
Decision Tree diagram to complete: